In mathematics, an integral assigns numbers to functions in a way that describes displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with differentiation, integration is a fundamental, essential operation of calculus, and serves as a tool to solve problems in mathematics and physics involving the area of an arbitrary shape, the length of a curve, and the volume of a solid, among others.

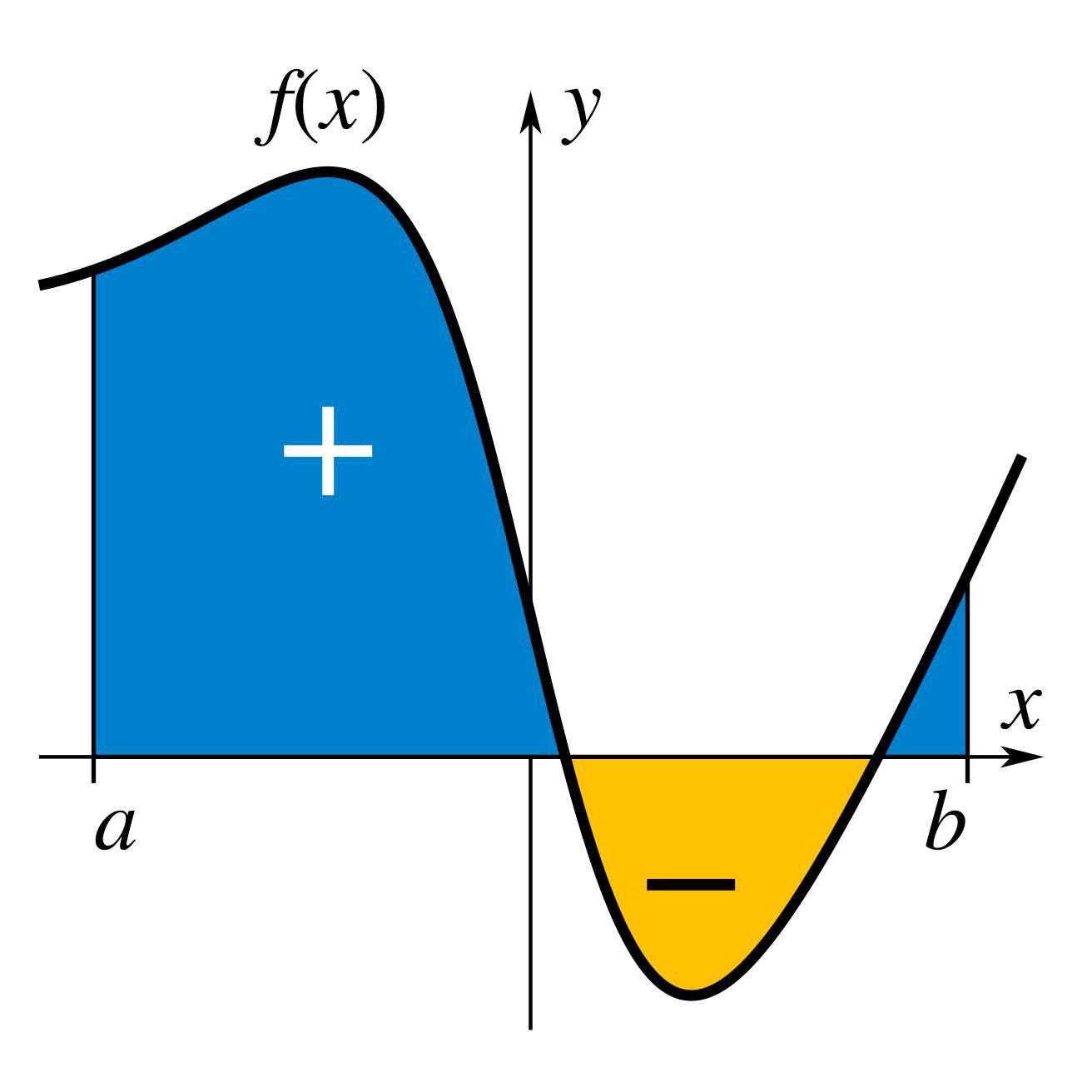
The integrals enumerated here are those termed definite integrals, which can be interpreted as the signed area of the region in the plane that is bounded by the graph of a given function between two points in the real line. Conventionally, areas above the horizontal axis of the plane are positive while areas below are negative. Integrals also refer to the concept of an antiderivative, a function whose derivative is the given function. In this case, they are called indefinite integrals. The fundamental theorem of calculus relates definite integrals with differentiation and provides a method to compute the definite integral of a function when its antiderivative is known.

Although methods of calculating areas and volumes dated from ancient Greek mathematics, the principles of integration were formulated independently by Isaac Newton and Gottfried Wilhelm Leibniz in the late 17th century, who thought of the area under a curve as an infinite sum of rectangles of infinitesimal width. Bernhard Riemann later gave a rigorous definition of integrals, which is based on a limiting procedure that approximates the area of a curvilinear region by breaking the region into infinitesimally thin vertical slabs. In the early 20th century, Henri Lebesgue generalized Riemann's formulation by introducing what is now referred to as the Lebesgue integral; it is more robust than Riemann's in the sense that a wider class of functions are Lebesgue-integrable.

Integrals may be generalized depending on the type of the function as well as the domain over which the integration is performed. For example, a line integral is defined for functions of two or more variables, and the interval of integration is replaced by a curve connecting the two endpoints of the interval. In a surface integral, the curve is replaced by a piece of a surface in three-dimensional space.

Gottfried Wilhelm (von) Leibniz (1 July 1646 [O.S. 21 June] – 14 November 1716) was a German polymath active as a mathematician, philosopher, scientist, and diplomat. He is a prominent figure in both the history of philosophy and the history of mathematics. He wrote works on philosophy, theology, ethics, politics, law, history, and philology. Leibniz also made major contributions to physics and technology, and anticipated notions that surfaced much later in probability theory, biology, medicine, geology, psychology, linguistics, and computer science. In addition, he contributed to the field of library science: while serving as overseer of the Wolfenbüttel library in Germany, he devised a cataloging system that would have served as a guide for many of Europe's largest libraries. Leibniz's contributions to this vast array of subjects were scattered in various learned journals, in tens of thousands of letters, and in unpublished manuscripts. He wrote in several languages, primarily in Latin, French and German, but also in English, Italian and Dutch.As a philosopher, he was one of the greatest representatives of 17th-century rationalism and idealism. As a mathematician, his greatest achievement was the development of the main ideas of differential and integral calculus, independently of Isaac Newton's contemporaneous developments. Mathematical works have consistently favored Leibniz's notation as the conventional expression of calculus.However, it was only in the 20th century that Leibniz's law of continuity and transcendental law of homogeneity found a consistent mathematical formulation by means of non-standard analysis. He was also a pioneer in the field of mechanical calculators. While working on adding automatic multiplication and division to Pascal's calculator, he was the first to describe a pinwheel calculator in 1685 and invented the Leibniz wheel, used in the arithmometer, the first mass-produced mechanical calculator. He also refined the binary number system, which is the foundation of nearly all digital (electronic, solid-state, discrete logic) computers, including the Von Neumann architecture, which is the standard design paradigm, or "computer architecture", followed from the second half of the 20th century, and into the 21st. Leibniz has been called the "founder of computer science".In philosophy and theology, Leibniz is most noted for his optimism, i.e. his conclusion that our world is, in a qualified sense, the best possible world that God could have created, a view sometimes lampooned by other thinkers, such as Voltaire in his satirical novella Candide. Leibniz, along with René Descartes and Baruch Spinoza, was one of the three great early modern rationalists. His philosophy also assimilates elements of the scholastic tradition, notably the assumption that some substantive knowledge of reality can be achieved by reasoning from first principles or prior definitions. The work of Leibniz anticipated modern logic and still influences contemporary analytic philosophy, such as its adopted use of the term "possible world" to define modal notions.